概要
「高分子の知識 気体透過性について(1)低分子の透過現象」では、”膜“に対する低分子の透過現象のイメージと対象材料について述べました。本資料では、引き続いて、非電荷膜での気体透過現象の機構について基礎的な事項について述べます。
気体透過性を評価するパラメーターとして透過係数があります。透過係数Pは、膜の単位面積あたり、単位時間あたりの面に垂直な方向の気体の流束(フラックス)Jから、
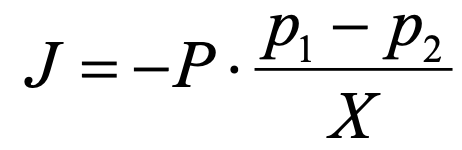 (1)
(1)
により、定義されます。ここで、p1は上流側の気体の圧力、p2は下流側の気体の圧力、Xは膜の厚みです。なお、膜の中で圧力の分布は無いと仮定しています。
図1に気体の透過を有孔性膜、無孔性膜について模式図を示しました。有孔性膜、多孔性膜の両方とも気体透過の原動力は、上流と下流との圧力差です。有孔性膜の場合は、孔の通過速度が透過性の違いに反映されます。無孔性膜の場合、膜表面への吸着と膜中の拡散と反対側の表面からの放散の違いが透過性の違いに反映されます。
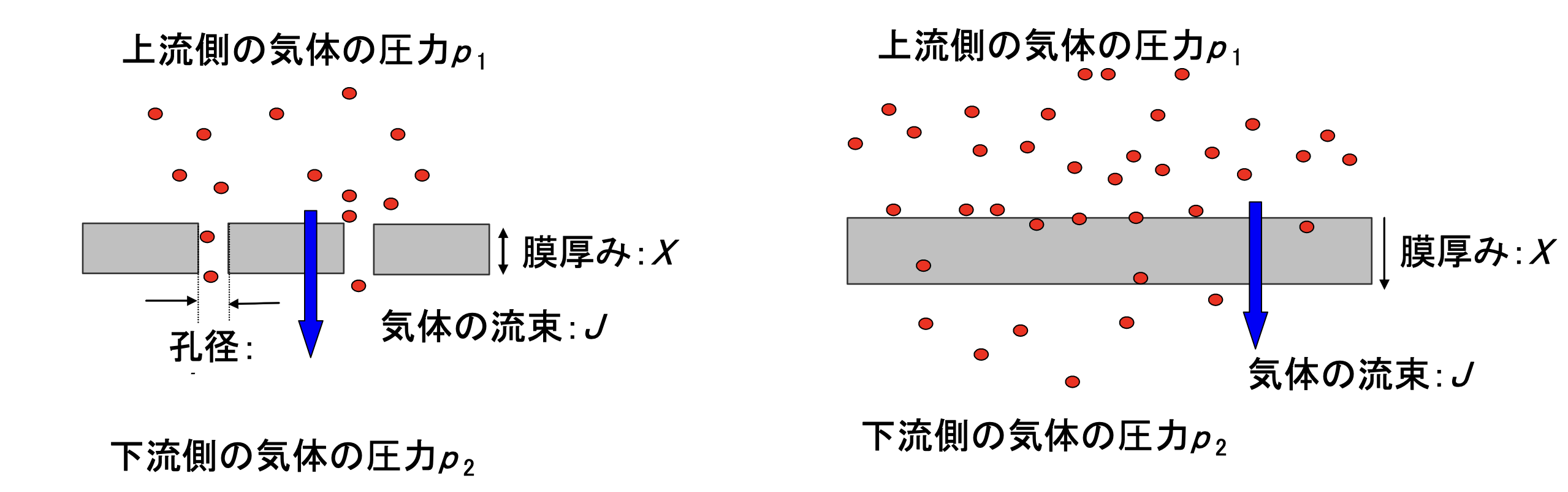
【図1】有孔性膜と無孔性膜での気体透過の模式図
孔が開いている場合は、気体分子は孔を通って透過する。孔がない場合、気体分子が固体膜に吸着・溶解して固体中を拡散して透過する。
膜の気体透過性を調べる上でまず確認しておかなければならないことは、孔があるかどうか、そしてその孔が、気体分子にとって大きいか小さいかです。
一般に、孔の径が気体分子の平均自由行程より小さくなる場合には、クヌッセン(Knudsen)流れ、それ以上になると、連続流体の流れであるハーゲン・ポアズイユ(Hagen-Poiseuille)流れとなります。平均自由行程は気体の圧力、時間、濃度によって変化します。概ね、孔径 1~2nmではクヌッセン流れ、孔径 2~5nmではハーゲン・ポアズイユ流れと考えてよいでしょう。なお、平均自由行程をλ、代表長さをLとするとλ/Lをクヌッセン数と呼びます。クヌッセン数が1以下であれば気体分子の流れを連続体として取り扱えます。クヌッセン流れでは透過係数![]() は気体の分子量
は気体の分子量![]() の-0.5乗に依存します。ハーゲン・ポアズイユ流れでは透過係数
の-0.5乗に依存します。ハーゲン・ポアズイユ流れでは透過係数![]() は気体の粘度
は気体の粘度![]() の-1乗に依存します。透過係数を測定して、そのどちらにも従わないとき、無孔性膜を気体が透過したとして取り扱うことが許されます。
の-1乗に依存します。透過係数を測定して、そのどちらにも従わないとき、無孔性膜を気体が透過したとして取り扱うことが許されます。
有孔性膜での透過現象は、気体分子の分離によく用いられます。この場合、クヌッセン流れが利用されますが、この際、表面拡散(あるいは、表面流れ)と呼ばれる現象が付随します。これは、気体分子がラングミューア(Langmuir)吸着などにより孔壁に吸脱着を繰り返しながら下流側へ移動する現象です。様々なモデルが提案されているようですが、詳細についてはここでは割愛します。
無孔性の膜での気体透過現象は、気体分子が固体表面に吸着し、固体中を拡散し、反対側の表面から放散される過程として捉えることができます。気相中に存在する気体分子と固相に溶解した気体分子が平衡状態にあるとすると、両者の“自由エネルギー(正確にはケミカルポテンシャル)”が等しい状態となります。低濃度では気体分子のケミカルポテンシャルは圧力、固体中の気体分子のケミカルポテンシャルは濃度![]() と等しくなります。したがって、圧力
と等しくなります。したがって、圧力![]() を変化させて、固体中の気体分子の濃度
を変化させて、固体中の気体分子の濃度![]() をプロットすると、
をプロットすると、![]() を溶解度係数として収着等温線
を溶解度係数として収着等温線
![]()
が得られることになります。ヘンリーの法則(Henry’s law)が成立すると![]() は定数ですが、ほとんどの場合は
は定数ですが、ほとんどの場合は![]() は
は![]() の複雑な関数となります。
の複雑な関数となります。
ガラス状の高分子固体への低分子の溶解については、気体の溶解現象で良く知られているヘンリーの法則に従うモードと、表面に存在すると考えられているミクロボイドへのラングミューア吸着によるモードの並列による二元輸送モデルが良く用いられます。
Henryの法則による吸着量 ![]()
Langmuir吸着による吸着量 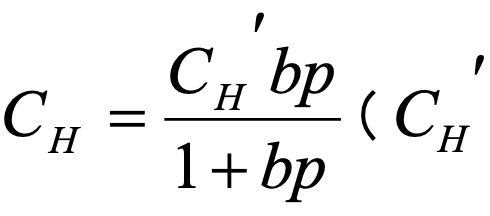 :飽和定数、:空孔親和定数と呼ばれる定数)
:飽和定数、:空孔親和定数と呼ばれる定数)
固相への吸着濃度 ![]()
このモデルはガラス状の高分子固体への低分子の吸収現象を良く再現する、優れた現象論モデルですが、高分子鎖の運動性などとの関連付けは、今日に至るまで良く分かっていないようです1)。
ここで、固体膜の上流側の表面では気体分子の濃度C1が、下流側の表面ではC2とします。固体膜の上流側から下流側まで分子が拡散した場合、拡散係数をDとして、フィック(Fick)型の拡散が成立すると、
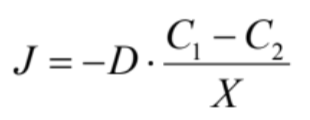 (2)
(2)
と書けます。この式を書き直すと、
式(1)から
ですので、次のように透過係数を書くことができます。
ここで、収着等温線![]() を考慮すると、
を考慮すると、![]() となるので、
となるので、
![]()
と書けます。これは、透過に対する溶解拡散機構の数式による表現です。
ゴム状高分子膜での透過機構のモデルには自由体積モデルが良く用いられます。これは低分子の自己拡散において高分子中を移動するにとき、系内の自由体積の配置換えにより低分子の移動に必要な空間が形成される必要があるという概念によって組み立てられています。
自由体積モデルと二元輸送モデルの最大の相違点は、二種の低分子成分が同時に拡散する混合透過の挙動にあります。自由体積モデルでは、混合成分のそれぞれが自由体積を持ち込むために、混合透過では単独透過よりも透過しやすくなります。また二元輸送モデルでは、混合成分が吸着サイトを奪い合うため、混合透過では単独透過よりも透過しにくくなります。
いずれのモデルも分子論的なパラメーターと結びつけて議論することは無理であり、あくまで現象論であることに注意が必要です。
参考文献
- 1) “Permeability of Polymer/ Clay Nanocomposites : A Review”: G.Choudalakis, A.D.Gotsis, Eur.Polym.J., 45, 967 (2009)
- 表面流れ(表面拡散)については、かなり古い文献であるが、次が参考になります。
- 2) “Membranes in Separations Chapter V Gaseous Diffusion”, S.-T.Hwang, K.Kammermeyer, John-Wiley & Sons New York (1975), P 52-66
