概要
第4回ではレオロジーのモデルと高分子材料の溶融液のレオロジー(粘弾性)について解説します。
5. レオロジーのモデルと高分子材料の溶融液のレオロジー
5.1. レオロジーの挙動を表すためのモデルと高分子材料融液のレオロジー挙動
図21や図22で示した弾性体のモデルは、図23のような変形と力が比例するバネやゴムを考えれば良いでしょう。また、図21や図22で説明したような塑性体は、図24に示すように平坦な面に置いた物体を動かすことを考えれば良いでしょう。粘性体のモデルはダッシュポットを考えることが多いですが、図25に示すように容器に水やシリコンオイルを入れ、その中に紐をつないだ鉄の球を入れて上下させることを考えれば良いでしょう。
変形すれば伸び、変形を取り除けば元に戻る
平面上の物体はある力を越えれば滑り出す。
水を容器に入れその中に鉄の球を入れ紐で釣り上げることを考える。
高分子材料のレオロジー(粘弾性)を再現するためにはこれらの要素を連結したモデルで現象を再現することができます。なお、この資料では高分子材料の融液のレオロジー挙動についての解説に絞ります。固体のレオロジーについては高分子物性の解説に譲ります。
高分子とは無限とも思える数の原子が結合した分子です。ブラウン運動をする紐あるいは鎖と考えることができます。高分子について表現するとき高分子鎖という言い方をすることが多いので、本資料でも高分子という書き方と高分子鎖と言う書き方が混在しています。
その中で最も成功したのはラウズモデルです。これは高分子のブラウン運動をバネとして表し、質量の無い球をつなぎ、球(ビーズ)が媒体から受ける抵抗を考えることで高分子の融液が示す粘弾性を再現するモデルです。この時の抵抗を摩擦係数ζとして表します。
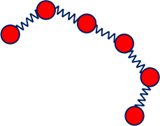
【図26】高分子鎖のバネ・ビーズモデル
質量のない球がフック則に従うバネで連結されていると考えます。
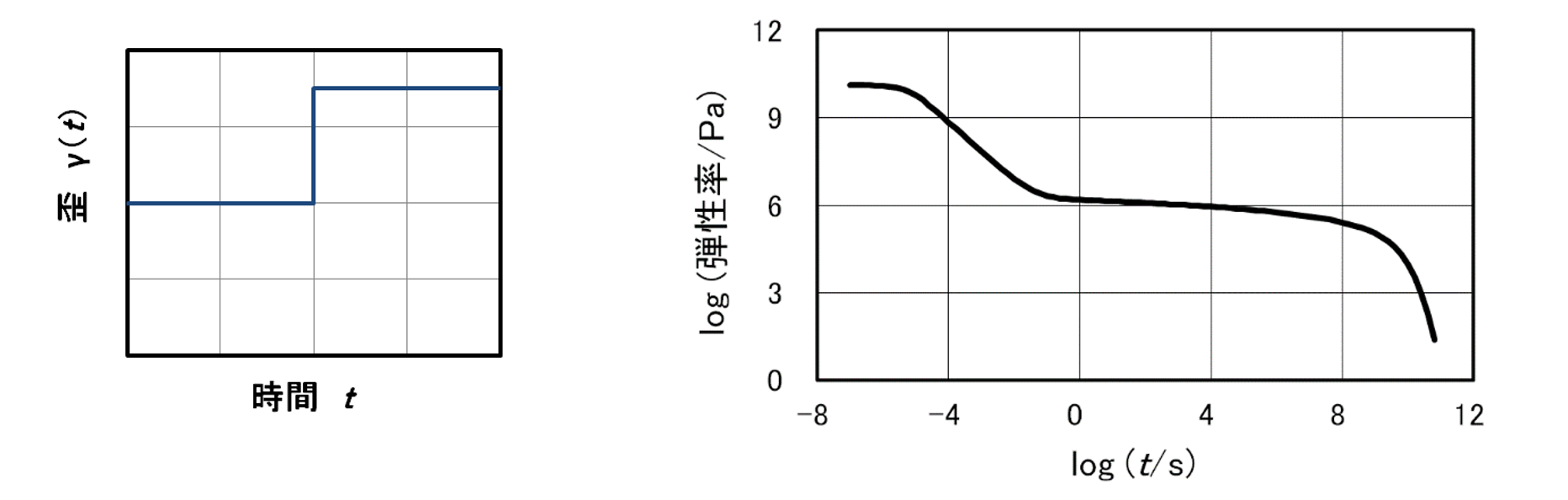
一定の歪みをある瞬間加えた場合、弾性率は時間に依存します。非常に短時間側と比較的長時間側に弾性率の時間依存性が緩やかな領域が存在します。短時間側がガラス状態、長時間側がゴム状態での弾性率となります。
さて、高分子の溶融体に、ある時間に一定の歪みを加えたときの挙動を応力と歪みの比である弾性率で表した場合のデータを図27に示しました。弾性率と時間を両対数プロットしています。弾性体であれば弾性率は時間が経過しても一定の値です。また粘性体であれば、一定の歪みを加えた際に一瞬応力が発生するだけですから弾性率としては時間の経過に関わらず0となります。しかし図27から判るように、弾性率が比較的一定な時間領域が2回ありますが、時間が経過すると0に近づきます。非常に長い時間が経てば粘性体ですが、弾性も示す時間域があるということで、粘弾性と呼ばれます。なお、この平坦に見える時間域での弾性率は各々ガラス状態、ゴム状態の弾性率と呼ばれます。ゴム状態の弾性率は分子量によらず、ポリエチレンやポリプロピレンというような高分子の種類によって決まる一定の値を取ります。
図27のような弾性率の挙動を示す高分子の溶融状態のモデル図を図28に示しました。
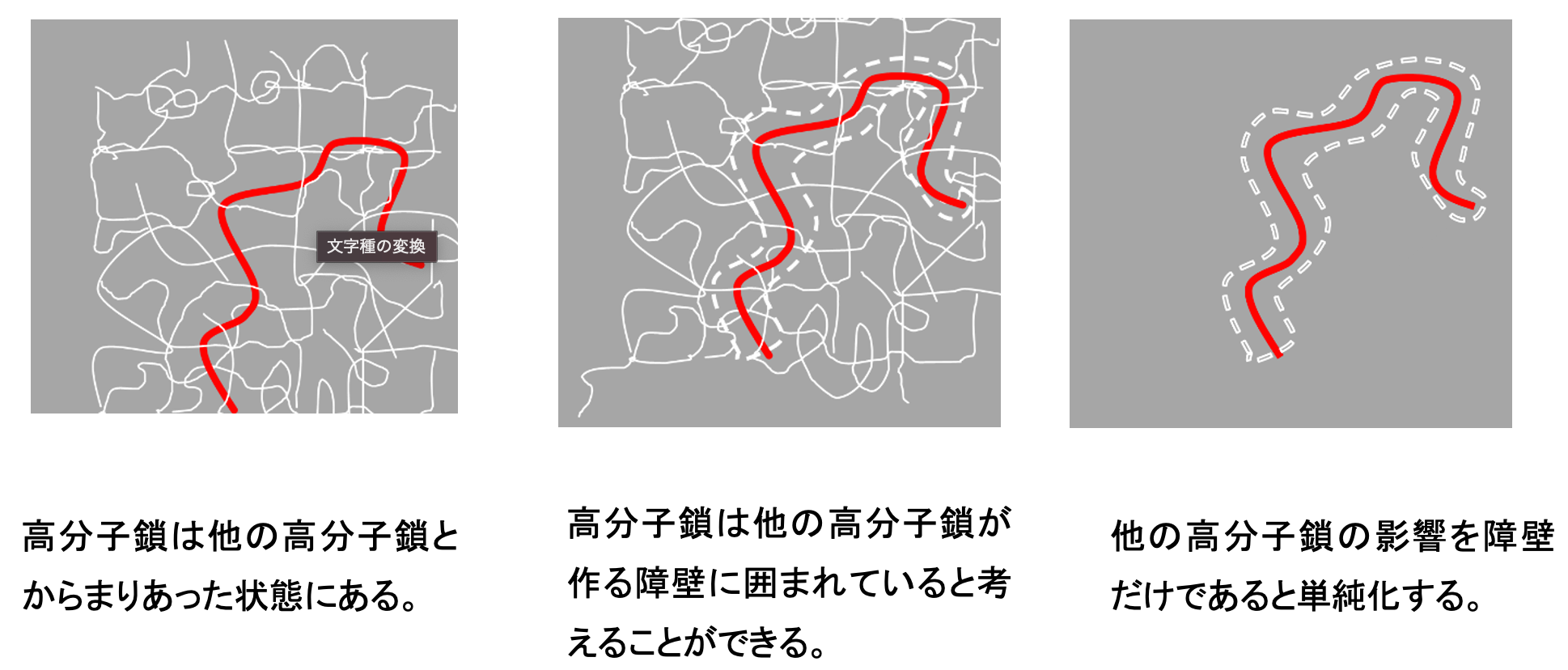
高分子鎖はお互いに動きを邪魔するため、溶融状態になっても容易に拡散できないため、ゴムに似た弾性を示す様になります。この状態を表すモデルが図28です。高分子鎖は障壁に囲まれてしまって、自分自身に沿った一次元の運動が一番速く進むことになってしまいます。単線の鉄道で列車は前後にしか動けない状況とよく似ています。このモデルをレプテーションモデル、管模型モデルと言います。このモデルでも高分子鎖の物理学的モデルとしては図26に示したようなバネ―ビーズモデルが使用されます。
5.2 高分子材料の融液のレオロジー挙動のモデル
レオロジーの測定で行われる変形としては、ある時刻に一定の歪みを瞬間的に与えて応力を測定し、弾性率の時間変化として観測する方法を図27で示しました。この他に図29で示すような周期的な歪み(黒線)を与えて観測する方法があります。この場合は歪みの振幅で応力を除した弾性率で評価します。青い実線で示した弾性体では与えた歪みと同じ周期で弾性率が振動します。青い点線で示した粘性体の場合は図で示したように周期が1/4周期だけ遅れた周期で振動します。赤い一点鎖線で示した粘弾性体の場合はこの中間の挙動を示します。この中間の挙動は弾性成分と粘性成分の二つに一義的に分解することができます。
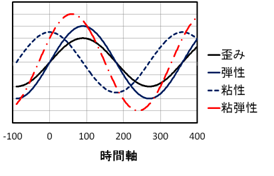
【図29】一定の角周波数で振動する歪みを与えた場合の弾性体と粘性体の挙動の模式図
図27での材料にこの方法を適用した場合は、図30のようなデータが得られます。弾性成分は白抜きの丸印で示した貯蔵弾性率、粘性成分は塗りつぶした丸印で示した損失弾性率と呼ばれます。与えた歪みの周期を角周波数ωで表すと、時間の逆数の単位を持ち、高い周波数が短時間側、低い値が長時間側に相当するデータとなります。
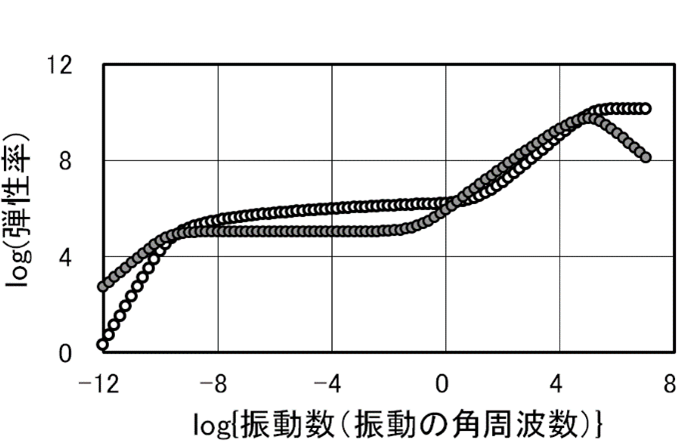
【図30】粘弾性体に振動する歪みを与えたときの弾性率の挙動
弾性性成分は○印で示した貯蔵弾性率、粘性成分は●で示した損失弾性率で表すことができる。
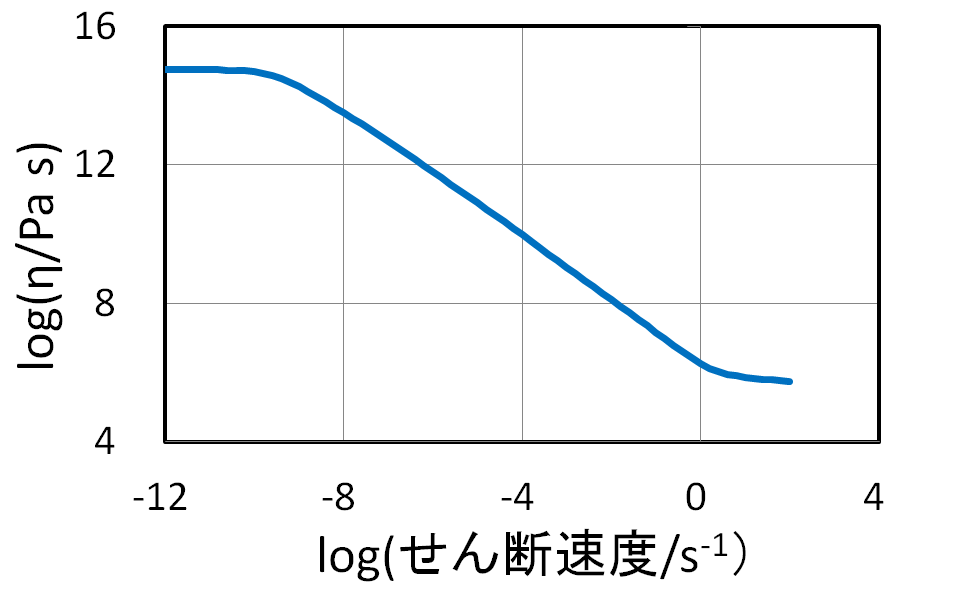
また、キャピラリーレオメーターで測定した場合、せん断速度に対して、粘度をプロットすると図31のようなデータが得られます。せん断速度が遅い場合、粘度がせん断速度に依存しない、ニュートン流動が観測されます。せん断速度を上げると、粘度は低下します。通常のキャピラリーレオメーターでは観測するのは困難ですが、さらに、高せん断速度領域では再びニュートン粘度が観測されます。(この現象は実験的に確認されています。)高分子の鎖が流動でからみ合いがほぐれ、鎖が伸び切り、鎖同士の摩擦だけが粘性発現の原因となるためであると考えられています。
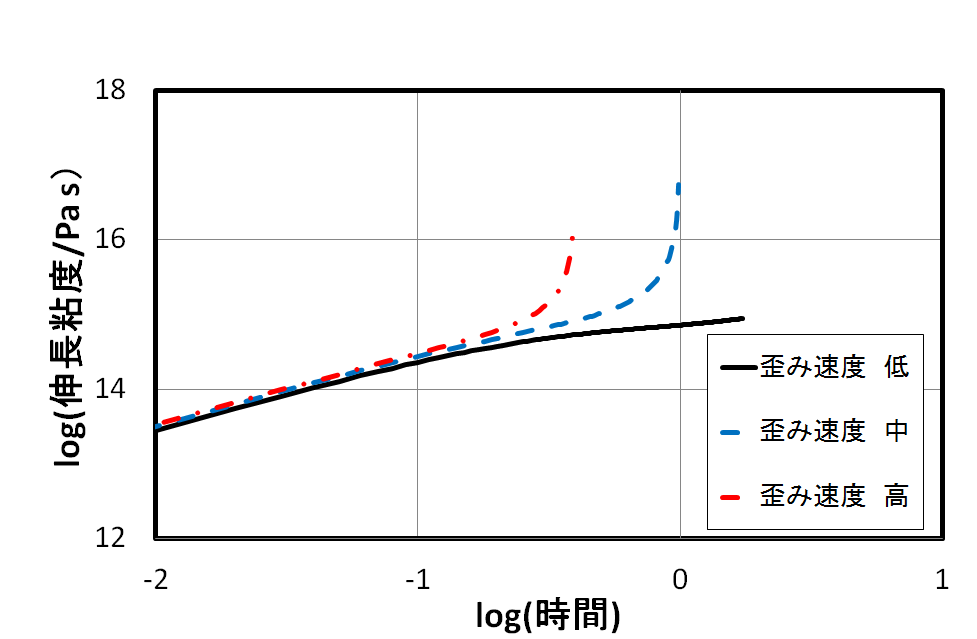
一軸伸長粘度では図32のように歪み速度に対して粘度をプロットするのではなく、時間に対するプロットをすることが普通です。これは歪み速度が高い場合、定常値を得ることが難しいためです。歪み速度が高くなると、図に示したように、伸長粘度は急速に立ち上がります。
この他、大変形の振動歪みを与えるようなLAOSや大変形を与えた緩和弾性率の観測などがレオロジー測定としてあります。ここでは説明を割愛します。
5.3 高分子材料溶融液のレオロジーの特徴
最後に高分子材料溶融液のレオロジーの特徴について簡単に述べます。
現在の理論ではゴム状領域の弾性率とバネビーズモデルの摩擦係数の二つだけをパラメーターとすることでレオロジーの特徴を記述することができることを述べました。このことは、高分子にはその分子種に依存せず、高分子であるがために生まれる特性があることを意味します。これを利用して標準品の検討から別の材料の特徴を予測することが可能になります。
この資料で示したレオロジー関数の特徴は高分子性を持つ限り、発現する特性です。特に図27や図30の短時間側(高周波数域)や長時間側(低周波数域)では、関数の形はポリマーによらずほぼ同一です。また、高分子性による運動モードが同一であれば、濃度や分子量、温度等が異なっても両対数グラフでは同じ関数形を示します。すなわち、実験的にはレオロジーは粘弾性のグラフを比較し、両対数プロットで重なり合う領域を求めることが一番初歩的な方法と言えるでしょう。
6. まとめ
レオロジーでの解析の前提となっている考え方と高分子の溶融体のレオロジーの入門の準備となると思われる解説をまとめました。
弊社では、一定の歪みを与えて測定する緩和弾性率、振動する歪みを加えて測定する貯蔵弾性率や損失弾性率、キャピラリーレオメーターを使用した粘度のせん断速度依存性の測定、さらには伸長粘度測定を受託しています。測定法や解析法に興味がある方は是非ご連絡ください。試料に適した測定法、解析法をご提案します。
さらに進んだ理解を目指すための参考書と参考文献は第1回の文末にまとめてあります。是非手に取ってみてください。



