概要
第3回ではレオロジーの測定について解説します。
4. レオロジーでの測定について
4.1. 測定する流動の様式
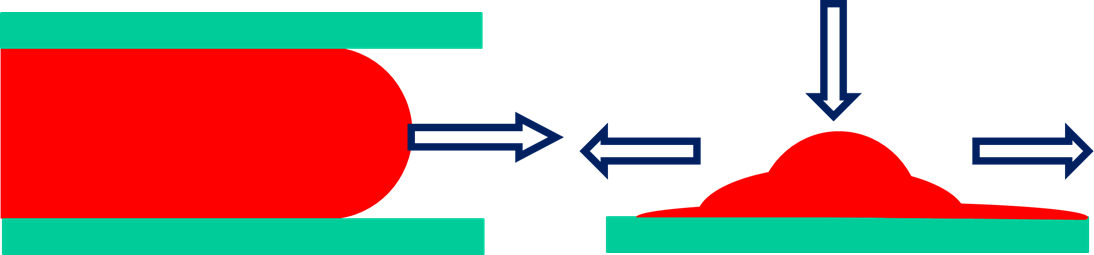
高分子材料の流れでは図13のように、壁に閉じ込められた状態と開放された状態での流れがあります。壁がある場合、例えば、川の流れを見てみると、両岸での流れが遅く、川の中央が早いように、壁があると壁に対する流体の見掛けの平均速度は0になります。また、開放された状態での流動では表面積が広がる動きがあって、表面張力との綱引きも考えなければならないことがあります。また、壁面との相性も問題になることがあります。この場合は、接触角の評価が重要になります。
平行な二つの壁に液体を挟み、片方の壁を動かすと、図14のような流れ方をします。この状態の流動を「せん断流動」と言います。別の言葉では「ずり流動」という言い方をします。この場合平行な二つの壁には挟まれていることからわかるように、流動中に材料の体積の変化はありません。
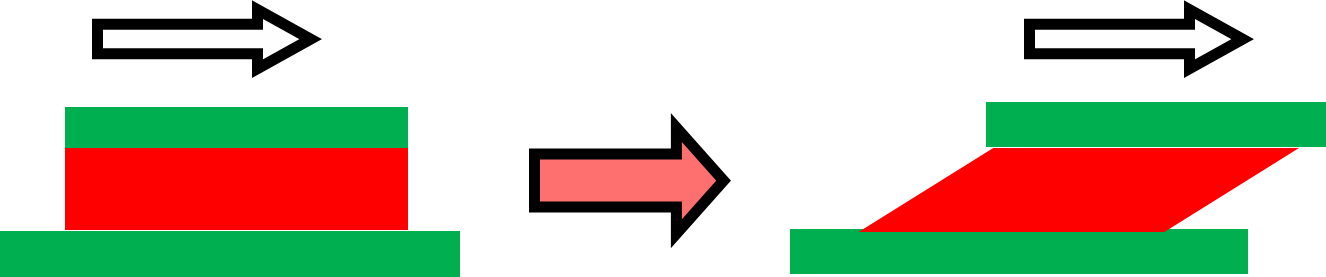
この流動の場合は、材料の体積の変化はありません。
図13の左側で示したような流動では、流速が十分低い場合、図14のせん断流動と同じ流れ方をしています。壁面での流速が0で中心での流速が最も速くなっています。
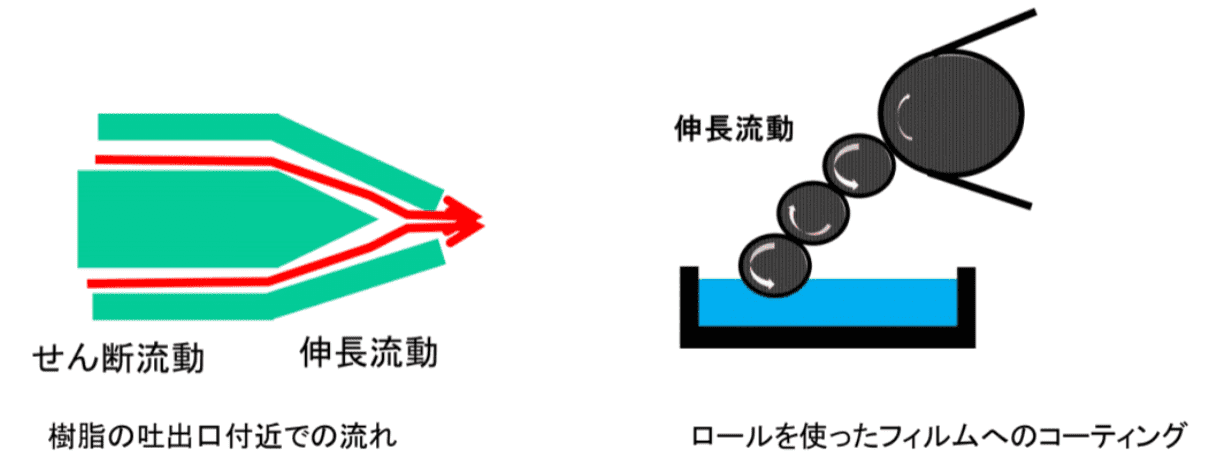
また図15に示したように、成形では合流する流れや自由表面を持つ流れもあります。その場合は、せん断流動だけではなく、図16のような一軸伸長流や一軸圧縮流動が起こります。このような伸長流動、圧縮流動は、表面積が広がるような流動です。このため、レオロジーを考えるとき、表面自由エネルギー(表面張力、界面張力)を考慮することが必要な場合もあります。特に、粘度が低い状態では表面自由エネルギーが支配的になります。
伸長流動は紡糸、フィルムの製造や容器のブロー成形あるいは発泡成形などで重要な役割を果たしています。そのため、評価が重要視される場合があります。伸長流動の場合、伸長される方向の変形が気になると思いますが、それと垂直側の変形も同時に起きています。伸長流動の場合、材料の体積が変化しなければ、材料が引っ張られる方向と垂直方向では収縮する、つまり、圧縮される必要があります。また、この垂直方向で収縮しなければ、材料の体積はどの方向にも膨張していることになります。
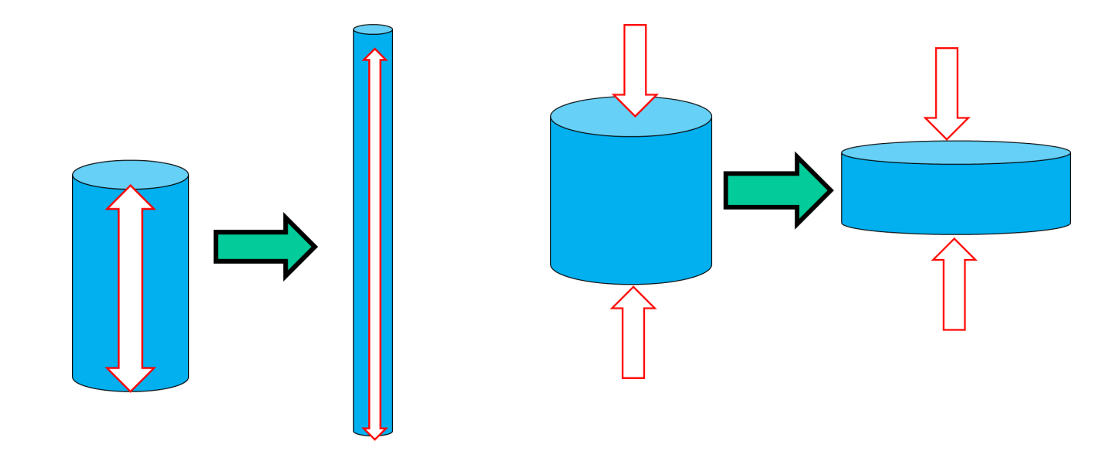
高分子材料の伸長流動や圧縮流動では変形の方向を示す矢印と垂直方向でも変形が起きています。
4.2. レオロジーで測定されるパラメーター
レオロジーの測定は、粘性率、弾性率、時間(緩和時間、遅延時間、流動開始あるいは流動停止後の時間)などの幾つかのパラメーターを相互に比較するグラフを書くことによって比較解析します。どのような装置を使っても、時間、変形量、力の大きさを記録します。変形を刺激とし、発生する力を測定することがほとんどですが、最近では力を刺激として変形を求める実験装置も多数市販されています。特に長い時間を要する測定の場合、力の方が測定の安定性が良いので、力を刺激とした測定が好まれる傾向にあります。
レオロジー測定をするためには変形や流れを再現する必要があります。レオロジーの測定装置の最も重要な部分は試料を測定する治具です。その方式は図17に示しました。図17-1では、オストワルドの粘度管のように毛管を用いる方式、図17-2ではB型粘度計のような二重の円筒と円筒の間に試料を装着する方式、図17-3と図17-4では各々、円錐と円板の間、あるいは円板と円板の間に試料を装着する方式を示しました。図17-5にはまた固化した状態あるいは高粘度のシートのストリップの両端を引っ張る方式を示ました。
図17-1に示した、毛管を用いる場合は、変形方式は管を流すだけで、測定の度に試料を入れ替える必要があります。それに対して、その他の装置は、連続的に回転する変形、あるいは振動する変形、瞬間的に一定の変形を与えるなど様々な変形を与えることができます、試料を入れ替えなくても測定は可能です。意図的に劣化しやすい条件で測定して、劣化を調べるようなことも可能です。
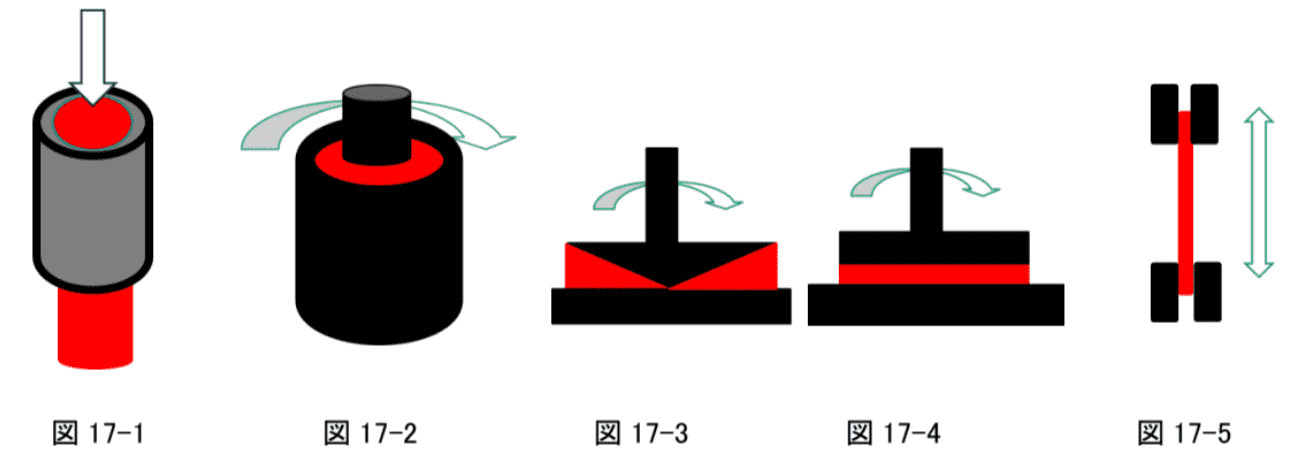
図17.粘弾性測定の主な方式
図17-1:毛管(キャピラリー)に樹脂を連続して流し込む方式。
図17-2:二重になった二つの円筒の間に樹脂を入れ、内筒あるいは外筒を回転あるいは振動させる方式。
図17-3:円錐と円板の間に樹脂を入れ、回転あるいは振動させる方式。
図17-4:円板と円板の間に樹脂を入れ、回転あるいは振動させる方式。
図17-5:試料の両端を引張り測定する方式。
4.3. レオロジー測定で得られる観測量(物理量とパラメーター)について
レオロジーでは、プラスチックス(合成樹脂、高分子材料、ポリマー材料)で起きている、変形と力の関係を調べることで、材料の解析を行います。ここでは、その際の変形と力の関係の解説を示しながら、レオロジーに必要な物理量やパラメーターについて解説します。
高分子材料のレオロジー特性は、変形を与えた後で変形を取り除いた場合、
・元に戻る図18の場合
・元に戻らない図19の場合
に大きく分けることができます。図19の場合、材料の周囲が容器で保護されていないと、変形を取り除くと形を保てない、図20で示した場合があります。それぞれの挙動を示す材料を“弾性体”、“塑性体”、“粘性体”と言います。理想的な場合は、弾性体は変形を取り除く瞬間に元の形に戻り、粘性体では瞬時に形を保てず、瞬時に流れ去ります。実際の材料は大なり小なりの時間依存性があります。例えば、図20の場合で1時間ぐらいでは流れ去ることは無いけれども、ひと月後に観察すると形が崩れていることがあります。
変形を取り除くと元に戻る場合
変形を取り除くと元に戻らない場合
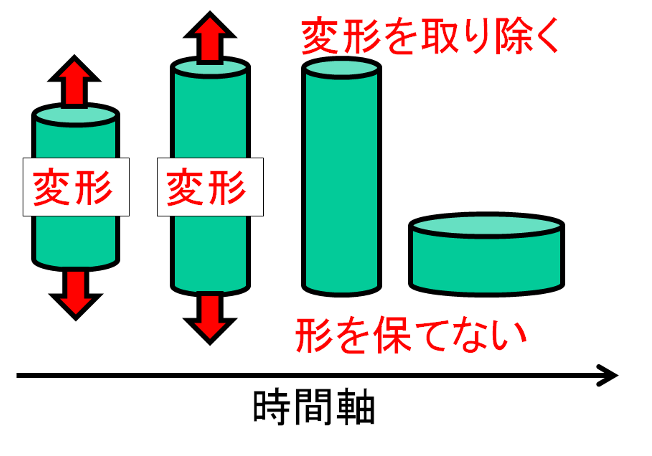
変形を取り除くと形を保てない場合
弾性体の例:ばね、輪ゴム
塑性体の例:粘土、パテ、練り歯磨き
粘性体の例:はちみつ、水
レオロジーではこのような変形の変化について、変形量ΔLと発生する力Fを考えます。それぞれは観測を始めてからの時間tについて記録できるので、そのことを示すため(時間tの関数として)変形量はΔL (t)、力はF(t)と書きます。
変形量は測定対象の材料が大きければ大きくなります。また力も測定対象の材料が大きくなれば大きくなります。材料の特性が変化していないのに変形量や、発生する力が変わるのでは、材料の特性の比較ができません。そこで、変形量は変形前の長さL0や変形の測定時の長さL (t)で割ります。これを歪と呼びます。
歪の定義 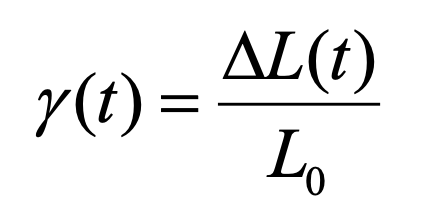 (2)
(2)
あるいは 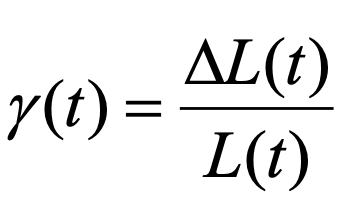 (3)
(3)
また力Fは、力が加わっている面の最初の面積S0あるいは力が発生している時の力が加わっている面積S(t)で除したパラメーターを使用します。これを応力と呼び、σと書きます。
応力の定義 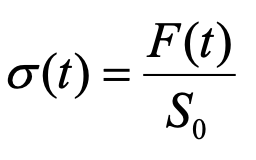 (4)
(4)
あるいは 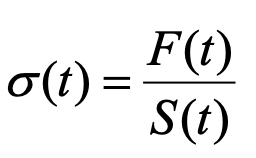 (5)
(5)
式(3)と式(5)とで定義される歪や応力が厳密な量です。しかし、工業的には式(2)及び式(4)で定義される歪や応力が使用されることの方が多いです。
レオロジーでの測定はまずはこの歪と応力の測定から始まります。歪については測定開始後からの変化速度、歪速度を問題にすることがあります。歪速度は次式で定義される、歪の時間に対する微分量です。
歪速度 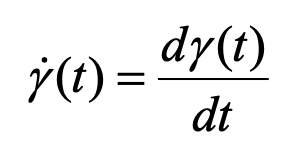 (6)
(6)
理想的な弾性体や粘性体で、歪、応力はどう変化するかを図21に示します。
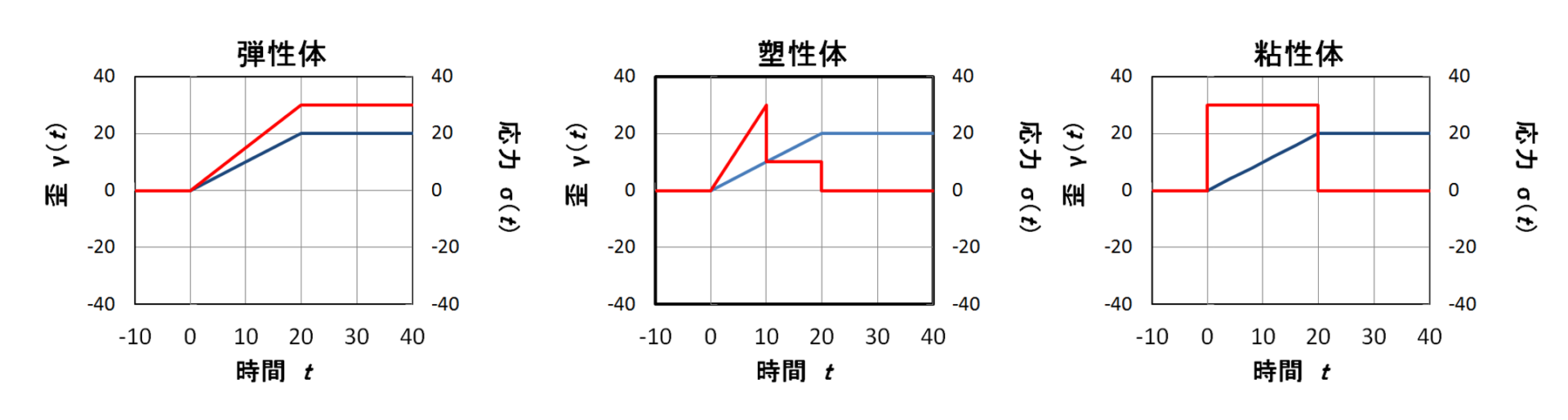
青線が歪γ、赤線が応力σを示します。歪が時間0から時間20までの間に徐々に大きくなり、時間20からは歪が一定に保たれると考えています。
図21では青線で示した歪が時間0から時間20までの間に徐々に大きくなり、時間20からは歪が一定に保たれると考えています。弾性体の場合、赤線で示した応力が一定の割合時間0から20までで大きくなります。ついで、塑性体ではある歪量10を超えると応力が一定の値まで瞬間的に低下します(これを降伏と呼びます。)。その後、一定の応力値を示しますが、歪みが時間に依存しなくなる時間20以上では応力が0となります。最後に、粘性体の場合は、歪みが大きくなる間は一定の応力が発生しますが、ひずみが時間に依存しなくなると応力は0になります。すなわち、弾性では変形によって材料に与えられたエネルギーが保存され、塑性体及び粘性体ではそのエネルギーが失われていることを示しています。その性質があるため、弾性的な性質には貯蔵、粘性的な性質には損失あるいは散逸という表現がされる場合があります。
図21から読み取れるように、弾性体については、応力と歪について
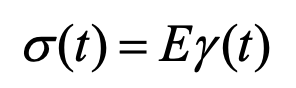 (7)
(7)
の比例関係が成り立ちます。この際の比例係数Eが弾性率です。また塑性体についてはある応力レベルσYまでは式(7)の関係が成り立ちます。この時の応力σYを降伏応力と言います。σY以上の応力では、流れている状態が観察されます。
粘性体の場合は一定の歪速度(図21での歪の時間に対する勾配)では、応力が一定となり、
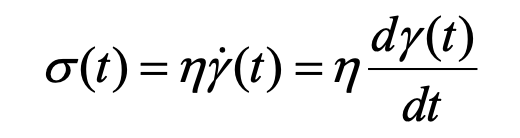 (8)
(8)
の比例関係が成り立ちます。この際の比例係数ηが粘度です。これらの関係を図22に示しました。
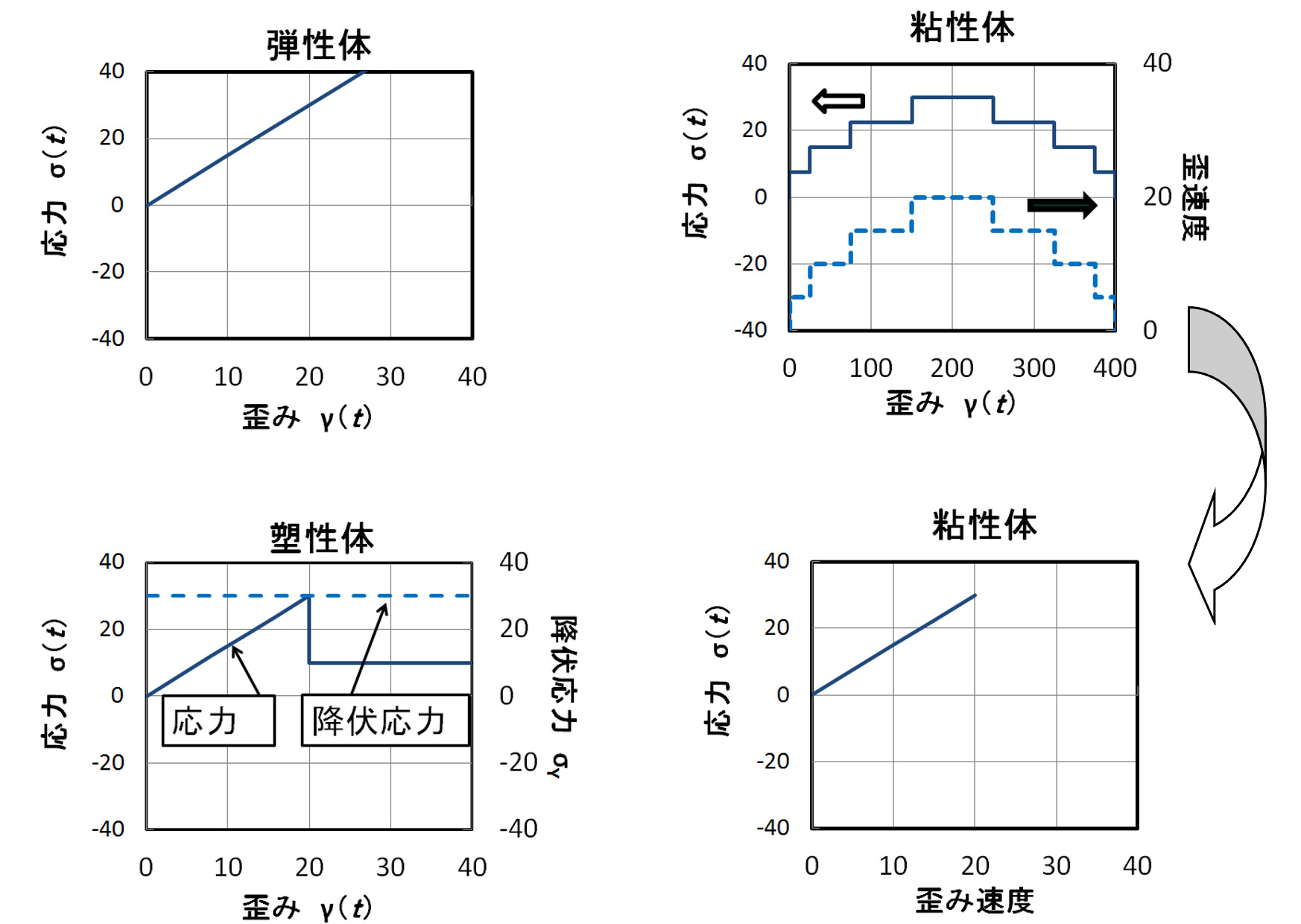
以上で示した、レオロジーで使用する主要なパラメーターをまとめると、応力、歪み、歪み速度、弾性率、粘度(粘性率)、降伏応力があります。複雑な系のレオロジーでは今までも説明では一定の値を持つ係数であったEあるいはηが時間tや歪γ、あるいは歪速度に依存すると上手く説明できる場合が多々あります。
さて、ここでの説明では歪みや応力について、ある一方向、例えば三次元空間のx軸に対してのみ考えています。そして、材料の体積変化を無視して記述しています。先に述べたように、体積変化の無い、せん断流動では、ここで示した考え方で実際の材料を扱うことができます。一方、伸長流動の場合は、材料の体積変化があっても無くても、x軸方向の変化のみ考えることができず、x軸方向と垂直なy軸方向、z軸方向の変化を考える必要が出てきます。


