ブラウン運動するコロイド粒子の大きさの表現方法Ⅰ

概要

　高分子の性質を理解するために必要な知識についてシリーズで解説していきます。
　第1回目は、高分子のサイズの意味を理解するため欠かせない微小球体のサイズについて述べます。なお、ここでいう微小サイズの意味は、ブラウン運動する球体であるという意味です。SEC（GPC）や高分子物性を理解するためには、この高分子のサイズは非常に重要な概念となります。
　本資料では、ストークス半径、粘度半径、回転半径（慣性半径）、熱力学的半径の順で述べて行きます。
　ストークスによると、半径αの球を粘度η₀の液体の中でゆっくりとした速度vで移動すると、流線の乱れにより抵抗力

（1）
が発生します。逆にある物体をこの粘度η₀の液体の中を速度vで移動したときに発生する抵抗力がf であるとき、その物体のサイズが半径αの球体と考えることが出来ます。これを流体力学的等価球と呼び、αをストークス半径あるいは流体力学的半径R_hと呼びます。

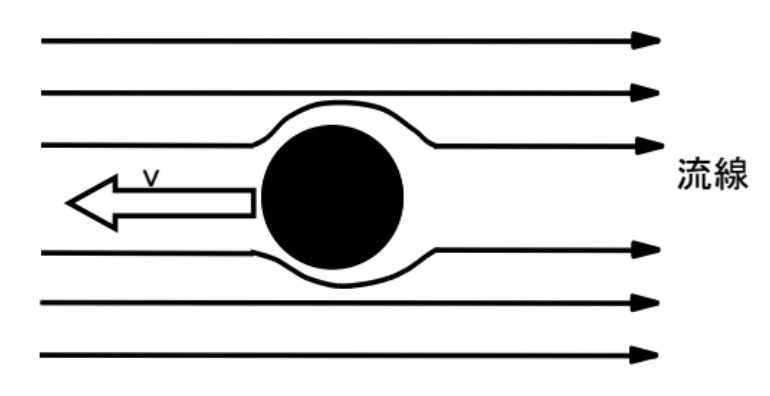
ブラウン運動を解析することで、球体の半径が拡散係数Dと関係することを示したのが、ストークス・アインシュタインの式

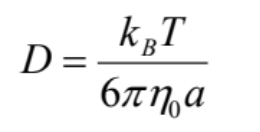（2）

です。この式からわかるように、ブラウン運動での拡散係数を求めることが出来れば、流体力学的等価球の半径を求めることが出来ます。
またEinsteinは球を含む液体の粘度ηが球の体積分率φのみで決まることを示しました。

（3）

球の濃度がc[g mL^-1]、分子量がMとすると、N_Aをアボガドロ数として、次式を用い、球の粘度半径R_ηを求めることが出来ます。

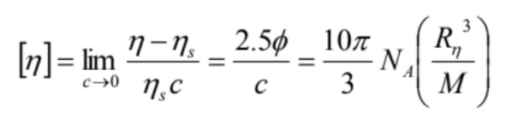
（N_A：アボガドロ数）（4）

実験的には、R_hとR_ηは同じと扱ってよいでしょう（参考文献1）。
光散乱の解析において、Zimmが定義した、Radius of Gyration（慣性半径あるいは回転半径）R_gは、その名称が予想させるような、回転モーメントに関係する量ではなく、重心からどの程度の距離の範囲に質量が存在しているかを示す量です。たとえば、半径の球について考えた場合、三次元での局座標を考え、その点での密度を考えると

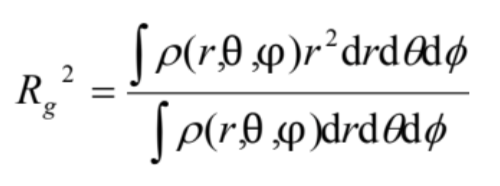（5）

で定義される量です。
半径αの球体を考えたとき、ストークス半径あるいは粘度半径はαとなりますが、回転半径は、0からαまの値を取りうることが出来ます。球体の構造によって、両者の関係は異なることがわかります。表1にρとαの関係の一例を示しました。

ただし、r=0～α

最後に熱力学的半径について説明します。溶液中の微小球体の濃度を考えるたとき、微小時間Δｔの間では、微小球体の濃度は均一ではなく、濃淡があります。そのとき、溶液中では浸透圧πが発生します。浸透圧πは、理想気体の状態方程式と全く同じ形式のvan’t Hoffの式

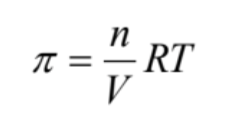（6）

（V：体積、ｎ：モル数、R：気体定数、T：絶対温度）
で表すことができます。

さて、理想気体と実在気体の相違点は、実在気体には分子同士の相互作用と、占有体積が存在することにあります。この点を考慮した式がvan der Waalsの式

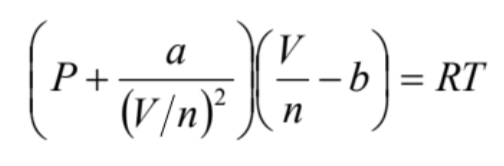（7）

（P：圧力、α、ｂ：相互作用に関係すると占有体積（正しくは排除体積）に関係するパラメーター）です。
圧力Pに対して、(V/n)=V_mに対して、ビリアル展開を行うことを考えます。
まず、（7）式を次のように書き換えます。

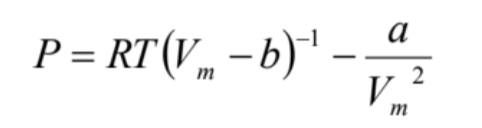（8）

V_mに対して、ｂは非常に小さいと考えることができます。この場合、数学的にはテイラー展開として知られる方法で展開すると、

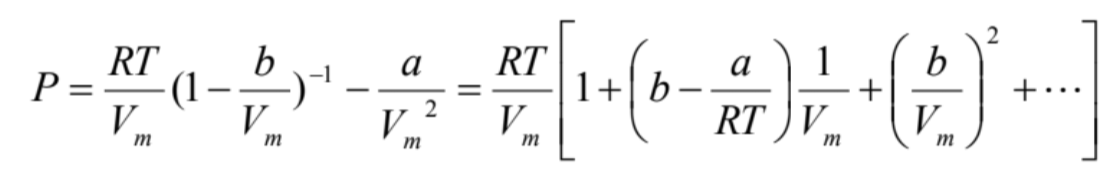（9）

と書けます。
浸透圧に関しても同じ考えを適用すると

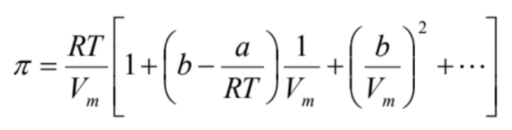（10）

と書けます。質量濃度c [g mL^-1]について書き直すと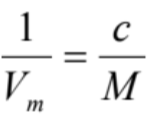であるので、

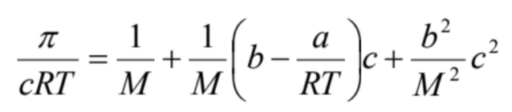（11）

と書き直せます。すなわち、第二ビリアル係数

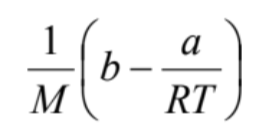（12）

は、微小球体の体積と、微小球体の間の相互作用に関係することがわかります。
厳密な理論は省略しますが、微小球が剛体球で相互作用が無い場合には、第二ビリアル係数は

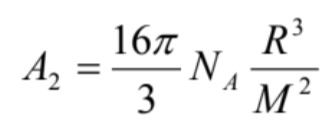、Rは剛体球の半径 （13）

と書けます（参考文献2の185ページ参照）。第二ビリアル係数に（13）式を適用して求める半径

（14）

を熱力学的等価球半径（thermodynamic equivalent radius）と呼びます（参考文献3）。

参考文献

• 1）J.EPuskas, E.A.Foreman, L.M.D.Santos, S.H.Soytas, Macromol. Symp., 261, 85 (2008)
• 2）H.Yamakawa, “Modern Theory of Polymer Solutions”, Electron Edition, Laboratory of Polymer Molecular Science, Department of Polymer Chemistry, Kyoto University (2001)
  （http://www.molsci.polym.kyoto-u.ac.jp/archives/redbook.pdf）
• 3）W.Burchard, Advances in Polymer Science, 143, 113 (1999)