概要
高分子の性質を理解するために必要な知識についてシリーズで解説しています。
第3回目は、第2回目に引き続き、高分子のサイズ(大きさ)を表現する方法である、回転半径と流体力学的半径について解説します。
さて、高分子は図1のように幾つかのセグメントが連結した構造でモデル化されます。

【図1】高分子のモデル
大きさ1のセグメントがnケ(今の図では50ケ)連結した鎖を考える。
この図では3次元での鎖をX-Y平面に投影した図を示している。
●印:末端(始点と終点)、■印:重心、●印同士を結ぶ矢印:末端間距離
このモデルで高分子の大きさを表すためのパラメーターとしては、まず、始点と終点の距離である、末端間距離“LEND-END”を考えることができます。高分子が分岐点を持たないような場合は良いのですが、分岐点を持つと末端は三つ以上になります。このとき、LEND-ENDを一義的に考えることができなくなります。また、この末端間距離に依存する物理量があまり知られていないので、実験的に決定することが難しいパラメーターです。
さて、各セグメントの両端に質点が存在するとして重心を考えることができます。
図1の場合、位置r0からr50までの51ケの同じ重さmのビーズが連結しているとみなせます。このとき、重心に対する二次モーメント、
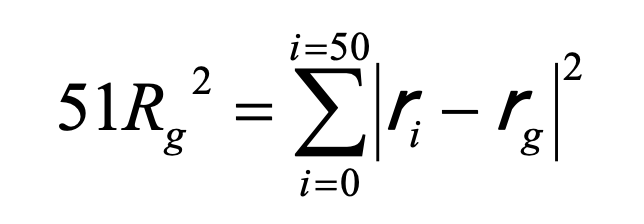 (1)
(1)
を考えることができます。なおrgは重心です。このRgを回転半径あるいは慣性半径と呼びます。この量は末端が幾つあっても計算できるので、高分子のサイズを表す量として、良く使われます。
ビーズが0からNまでである場合には
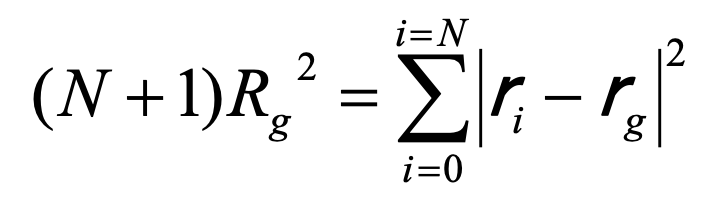 (2)
(2)
と書くことができます。この(2)式は、重心の定義式
(3)
を用いると
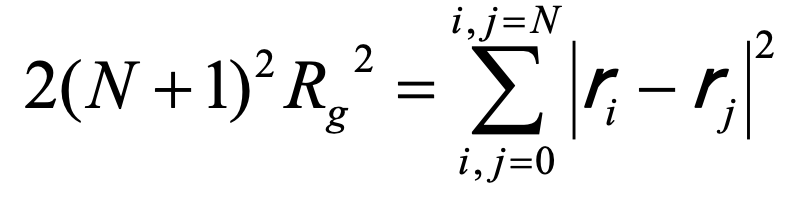 (4)
(4)
と書けます。
一方、高分子が粘度η0の溶媒中に少数、つまりお互いに接触するこがほとんどない程度に存在する場合を考えます。ビーズの間の流体力学的な相互作用から、Kirkwood-Risemannは、高分子を球体と考えた場合のストークス半径を計算しました。この半径を流体力学的半径Rhと呼び、次の結果を示しています。
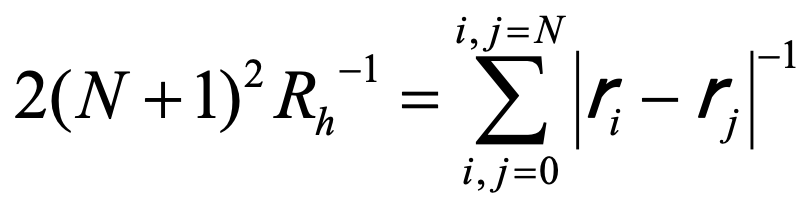 (4)
(4)
図1のようなモデルで計算すると、各々の平均値に対して、
![]() (5)
(5)
が得られ、流体力学的半径の方が小さくなります。
完全な剛体球であれば、高分子の知識(1)の表1で示したように、となります。したがって、図1のようなモデルに対して流体力学的等価球として考えると、図2のように、高分子と溶媒が一体になって動く球の部分ができて、その球の外にセグメントが飛び出して、溶媒の流れの影響を受けているモデルが描けます。

【図2】高分子の形成する流体力学的等価球のモデル
薄い青い部分が流体力学的等価球で、この中には溶媒は高分子と一体となって動く。
参考文献
| 1) | J.G.Kirkwood, J.Riseman, J.Chem.Phys.,16, 565 (1948) |
| 2) | I.Teraoka, Macromolecules,37, 6632 (2004) |
| 3) | I.Teraoka, “Polymer Solutions”, John Wiley, (2002) |
