概要
高分子の性質を理解するために必要な知識についてシリーズで解説しています。
第2回目は、高分子のサイズ(大きさ)を表現する方法である固有粘度について解説します。
固有粘度の求め方を述べた後、一点法について紹介します。末尾の【補足】で固有粘度が負になる現象について文献を紹介します。
固有粘度は高分子の解析を行う上で、重要なパラメーターです。固有粘度は物体をある溶媒に溶解した溶液において、一般に粘度が溶媒から上昇する現象に基づいて算出されます。すなわち、溶媒の粘度をη0、濃度c g mL-1の際の粘度をηとして、固有粘度[η]は、濃度を薄めながら粘度ηを、比粘度 ![]() を濃度cで除した量、
を濃度cで除した量、![]() 濃度0へ外挿して得られる量です。
濃度0へ外挿して得られる量です。
濃度と粘度の関係から固有粘度を求める式は種々提案されています。教科書では次の二つの式が取り上げられ、それぞれの濃度依存性が逆になることを利用して、濃度0への外挿を容易にできる方法として採用されていると思います。
Hugginsの式1) 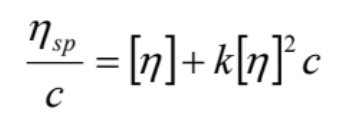 (1)
(1)
Mead and Fuossの式2) 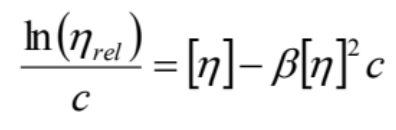 (2)
(2)
η0: 溶媒の粘度、c g mL-1: 溶質の濃度、η:溶液の粘度、
![]() :相対粘度、
:相対粘度、![]() :比粘度
:比粘度
その他にも、濃度0へ外挿して固有粘度を求めるための式が提案されています。代表的な例を挙げてみました。
Shultz and Blaschkeの式3) 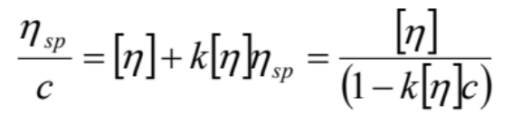 (3)
(3)
Staudinger and Henserの式4)![]() (4)
(4)
Martinの式5)![]() (5)
(5)
Arrhenius,Rother and Hoffmannの式6)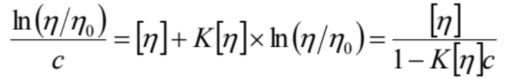 (6)
(6)
Schrameckの式7) ![]() (7)
(7)
Sakaiの検討結果によれば、濃度0に外挿する際の最も優れる式は、Martinの式です8)。(良く見ると式(4)と式(5)は同じです。Sakai以外の文献でも、Martinの式の方が引用されることが多いようです。理由は良く分かりません。)
さて、簡便のため、濃度1点で測定する方法が色々と提案されています。これらの中で有効な方法としては、次の式があります。
Solomon-Cuita9)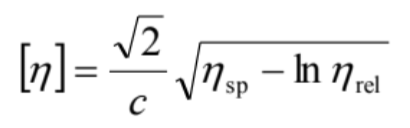 (8)
(8)
F.W.Billmeyer,Jr10)
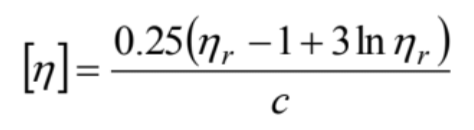 (9)
(9)
Fikentscher11) 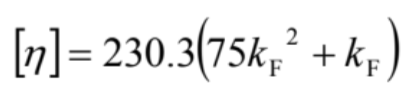 (10)
(10)
ただし、kFは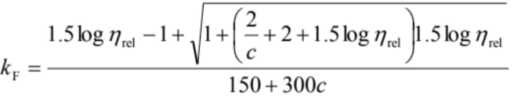 によって求める。
によって求める。
これらは、式(8)と(9) は、ηsp<0.6であれば、誤差5 %以下となり、(C)式はηsp=1.5程度の値の場合に誤差が5 %以下となります12)。なおR.PamiesらもSolomon-Cuitaの式(10)の誤差について論じた報告を提出しています。
各種規格の中では
式(8)はJIS K 6720-2:1999 (ISO-1060-2:1998)「プラスチック-塩化ビニルホモポリマー及びコポリマー (PVC) -第2部: 試験片の作り方及び諸性質の求め方」で採用されています。
式(9)はASTM D4603 – 03 “Standard Test Method for Determining Inherent Viscosity of Poly(Ethylene Terephthalate) (PET) by Glass Capillary Viscometer”で採用されています。
式(10)はK 7367-1:2002(ISO 1628-1:1998) 「 プラスチック-毛細管形粘度計を用いたポリマー希釈溶液の粘度の求め方-第1部:通則」に採用されています。
参考文献
| 1) | M.L.Huggins, J.Amer.Chem.Soc., 64, 2716 (1942) |
| 2) | E.O.Kraemer, Ind.Eng.Chem.,30, 1200 (1938) |
| 3) | G.V.Schlutz, F.Blaschke, J.Prakt.Chem.,158,130 (1941) |
| 4) | H.Staudinger and W.Heuer, Z.Physik.Chem., A171, 129 (1934) |
| 5) | A.F.Martin, Am.Chem.Soc.meeting, Memphis, 1942; discussed by M.L.Huggins in Cellulose and Cellulose Derivertives (High Polymers, 5,) E.Ott, Ed., Inter-science, New York, 1943, pp.966 -971 A.F.Martin, Tappi, 34 (8), 363 (1951) |
| 6) | M.Hoffmann, Makromol.Chem., 24, 222 (1957) |
| 7) | W.Scrameck, Macromol. Chem., 17, 19 (1955) |
| 8) | T.Sakai, J.Polym.Sci.: Part A2, 6, 1659 (1968) |
| 9) | Solomon, O. F; Ciuta, I. Z.: J. Appl. Polym. Sci, 6, 683 (1962) |
| 10) | F.W.Billmeyer,Jr, J.Polym.Sci., Ⅳ, 83-86 (1949) |
| 11) | Fikentscher, von H.: Cellul. Chem., 13, 58 (1931) |
| 12) | 高取永一, 志村尚俊, 日本ゴム協会誌, 81, 211 (2008) |
| 13) | R.Pamies, J.G.H.Cifre, M.delC.L.Martinez,J.C.delaTorre, Colloid & Polym.Sci., 286, 1223 (2008) |
【補足】
[η]は常に正とは限りません。オリゴマーの領域で負になる場合が知られていますA1)。
| A1) | X.Yang, S.-Q.Wang, Macromolecules, 33, 3128 (2000) |
